3.11 Related Rates
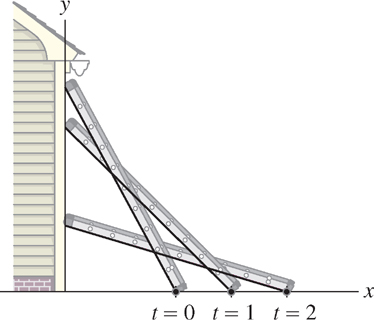
In related-rate problems, the goal is to calculate an unknown rate of change in terms of other rates of change that are known. The “sliding ladder problem” is a good example: A ladder leans against a wall as the bottom is pulled away at constant velocity. How fast does the top of the ladder move? What is interesting and perhaps surprising is that the top and bottom travel at different speeds. Figure 3.64 shows this clearly: The bottom travels the same distance over each time interval, but the top travels farther during the second time interval than the first. In other words, the top is speeding up while the bottom moves at a constant speed. In the next example, we use calculus to find the velocity of the ladder’s top.
EXAMPLE 1 Sliding Ladder Problem
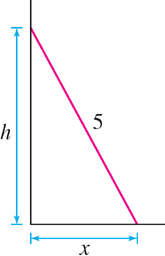
A 5-meter ladder leans against a wall. The bottom of the ladder is 1.5 meters from the wall at time \(t = 0\) and slides away from the wall at a rate of 0.8 m/s. Find the velocity of the top of the ladder at time \(t = 1\).
Solution The first step in any related-rate problem is to choose variables for the relevant quantities. Since we are considering how the top and bottom of the ladder change position, we use variables (Figure 3.65):
- \(x = x(t)\) distance from the bottom of the ladder to the wall
- \(h = h(t)\) height of the ladder’s top
Both \(x\) and \(h\) are functions of time. The velocity of the bottom is \(\frac{dx}{dt} = 0.8\text{ m/s}\). The unknown velocity of the top is \(\frac{dh}{dt}\), and the initial distance from the bottom to the wall is \(x(0) = 1.5\), so we can restate the problem as
\[ \boxed{\text{Compute }\dfrac{dh}{dt}\text{ at }t=1\text{ given that }\dfrac{dx}{dt}=0.8\text{ m/s and }x(0)=1.5\text{ m}} \]
To solve this problem, we need an equation relating \(x\) and \(h\) (Figure 3.65). This is provided by the Pythagorean Theorem:
\[ x^{2} + h^{2} = 5^{2} \]
To calculate \(\frac{dh}{dt}\), we differentiate both sides of this equation with respect to \(t\):
\begin{align*} \frac{d}{dt}x^2 + \frac{d}{dt}h^2 &= \frac{d}{dt}5^2\\ 2x\frac{dx}{dt} + 2h\frac{dh}{dt} &= 0 \end{align*}
196
| \(t\) | \(x\) | \(h\) | \(\frac{dh}{dt}\) |
|---|---|---|---|
| 0 | 1.5 | 4.77 | −0.25 |
| 1 | 2.3 | 4.44 | −0.41 |
| 2 | 3.1 | 3.92 | −0.63 |
| 3 | 3.9 | 3.13 | −1.00 |
This table of values confirms that the top of the ladder is speeding up.
Therefore \(\frac{dh}{dt}=-\frac{x}{h}\frac{dx}{dt}\), and because \(\frac{dx}{dt}=0.8\text{ m/s}\), the velocity of the top is
\[ \boxed{\dfrac{dh}{dt}= -0.8\dfrac{x}{h}\text{ m/s}}\tag{1} \]
To apply this formula, we must find \(x\) and \(h\) at time \(t = 1\). Since the bottom slides away at 0.8 m/s and \(x(0) = 1.5\), we have \(x(1) = 2.3\) and \(h(1) = \sqrt{5^2-2.3^2}\approx 4.44\). We obtain (note that the answer is negative because the ladder top is falling):
\[ \left.\frac{dh}{dt}\right|_{t=1} = -0.8\frac{x(1)}{h(1)}\approx -0.8\frac{2.3}{4.44}\approx -0.41\text{ m/s} \]
CONCEPTUAL INSIGHT
A puzzling feature of Eq. (1) is that the velocity \(\frac{dh}{dt}\), which is equal to \(-0.8\frac{x}{h}\), becomes infinite as \(h \rightarrow0\) (as the top of the ladder gets close to the ground). Since this is impossible, our mathematical model must break down as \(h \rightarrow 0\). In fact, the ladder’s top loses contact with the wall on the way down and from that moment on, the formula is no longer valid.
In the next examples, we divide the solution into three steps that can be followed when working the exercises.
EXAMPLE 2 Filling a Rectangular Tank
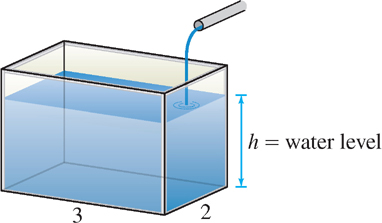
Water pours into a fish tank at a rate of \(0.3\text{ m}^{3}\text{/min}\). How fast is the water level rising if the base of the tank is a rectangle of dimensions \(2 \times 3\) meters?
Solution To solve a related-rate problem, it is useful to draw a diagram if possible. Figure 3.66 illustrates our problem.
Step 1. Assign variables and restate the problem.
It is helpful to choose variables that are related to or traditionally associated with the quantity represented, such as \(V\) for volume, for an angle, \(h\) or \(y\) for height, and \(r\) for radius.
First, we must recognize that the rate at which water pours into the tank is the derivative of water volume with respect to time. Therefore, let \(V\) be the volume and \(h\) the height of the water at time \(t\). Then
\begin{align*} \frac{dV}{dt}&=\text{rate at which water is added to the tank}\\[5pt] \frac{dh}{dt}&=\text{rate at which the water level is rising} \end{align*}
Now we can restate our problem in terms of derivatives:
\[ \boxed{\text{Compute }\dfrac{dh}{dt}\text{ given that }\dfrac{dV}{dt}=0.3\text{ m}^{3}\text{/min}} \]
Step 2. Find an equation relating the variables and differentiate.
We need a relation between \(V\) and \(h\). We have \(V = 6h\) since the tank’s base has area \(6 \text{ m}^{2}\). Therefore,
\[ \frac{dV}{dt} = 6 \frac{dh}{dt}\implies\frac{dh}{dt} = \frac{1}{6}\frac{dV}{dt} \]
Step 3. Use the data to find the unknown derivative.
Because \(\frac{dV}{dt} = 0.3\), the water level rises at the rate
\[ \frac{dh}{dt} = \frac{1}{6}\frac{dV}{dt} = \frac{1}{6}(0.3) = 0.05\text{ m/min} \]
Note that \(\frac{dh}{dt}\) has units of meters per minute because \(h\) and \(t\) are in meters and minutes, respectively.
197
The set-up in the next example is similar but more complicated because the water tank has the shape of a circular cone. We use similar triangles to derive a relation between the volume and height of the water. We also need the formula \(V=\frac{1}{3}\pi hr^2\) for the volume of a circular cone of height \(h\) and radius \(r\).
EXAMPLE 3 Filling a Conical Tank
Water pours into a conical tank of height 10 m and radius 4 m at a rate of \(6 \text{ m}^{3}\text{/min}\).
(a) At what rate is the water level rising when the level is 5 m high?
(b) As time passes, what happens to the rate at which the water level rises?
Solution
(a) Step 1. Assign variables and restate the problem.
As in the previous example, let \(V\) and \(h\) be the volume and height of the water in the tank at time \(t\). Our problem, in terms of derivatives, is
\[ \boxed{\text{Compute }\dfrac{dh}{dt}\text{ at }h=5\text{ given that }\dfrac{dV}{dt}=6 \text{ m}^{3}\text{/min}} \]
Step 2. Find an equation relating the variables and differentiate.
When the water level is \(h\), the volume of water in the cone is \(V=\frac{1}{3}\pi hr^2\), where \(r\) is the radius of the cone at height \(h\), but we cannot use this relation unless we eliminate the variable \(r\). Using similar triangles in Figure 3.67, we see that
\[ \frac{r}{h} = \frac{4}{10} \]
or
\[ r = 0.4h \]
CAUTION A common mistake is substituting the particular value \(h = 5\) in Eq. (2). Do not set \(h =5\) until the end of the problem, after the derivatives have been computed. This applies to all related-rate problems
Therefore,
\begin{align*} V&=\frac{1}{3}\pi h (0.4h)^2 = \left(\frac{0.16}{3}\right)\pi h^3\\[5pt] \frac{dV}{dt}&=(0.16)\pi h^2\frac{dh}{dt}\tag{2} \end{align*}
Step 3. Use the data to find the unknown derivative.
We are given that \(\frac{dV}{dt}=6\). Using this in Eq. (2), we obtain
\begin{align*} (0.16)\pi h^2\frac{dh}{dt}&=6 \\[5pt] \frac{dh}{dt}&=\frac{6}{(0.16)\pi h^2}\approx \frac{12}{h^2}\tag{3} \end{align*}
When \(h = 5\), the level is rising at a rate of \(\frac{dh}{dt}\approx \frac{12}{5^2} = 0.48\text{ m/min}\).
(b) Eq. (3) shows that \(\frac{dh}{dt}\) is inversely proportional to \(h^{2}\). As \(h\) increases, the water level rises more slowly. This is reasonable if you consider that a thin slice of the cone of width \(\Delta h\) has more volume when \(h\) is large, so more water is needed to raise the level when \(h\) is large (Figure 3.68).
198
EXAMPLE 4 Tracking a Rocket
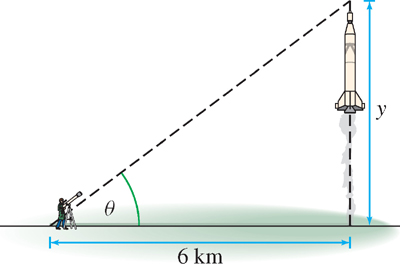
A spy uses a telescope to track a rocket launched vertically from a launching pad 6 km away, as in Figure 3.69. At a certain moment, the angle \(\theta \) between the telescope and the ground is equal to \(\frac{\pi}{3}\) and is changing at a rate of 0.9 rad/min. What is the rocket’s velocity at that moment?
Solution
Step 1. Assign variables and restate the problem.
Let \(y\) be the height of the rocket at time \(t\). Our goal is to compute the rocket’s velocity \(\frac{dy}{dt}\) when \(\theta = \frac{\pi}{3}\) so we can restate the problem as follows:
\[ \boxed{\text{Compute }\left.\dfrac{dy}{dt}\right|_{\theta=\frac{\pi}{3}}\text{ given that }\dfrac{d\theta}{dt}=0.9\text{ rad/min when }\theta=\frac{\pi}{3}} \]
Step 2. Find an equation relating the variables and differentiate.
We need a relation between \(\theta\) and \(y\). As we see in Figure 3.69,
\[ \tan\theta = \frac{y}{6} \]
Now differentiate with respect to time:
\begin{align*} \sec^2\theta\frac{d\theta}{dt}&=\frac{1}{6}\frac{dy}{dt}\\[5pt] \frac{dy}{dt}&=\frac{6}{\cos^2\theta}\frac{d\theta}{dt}\tag{4} \end{align*}
Step 3. Use the given data to find the unknown derivative.
At the given moment, \(\theta = \frac{\pi}{3}\) and \(\frac{d\theta}{dt}= 0.9\), so Eq. (4) yields
\[ \frac{dy}{dt} = \frac{6}{\cos^2(\pi/3)}(0.9) = \frac{6}{(0.5)^2}(0.9) = 21.6\text{ km/min} \]
The rocket’s velocity at this moment is 21.6 km/min, or approximately 1296 km/h.
Question 3.26 Related Rates Progress Check 1
NlA8pkFqn+sm0xpmztRRC4x/7sINr7ywc/uzsxy2GrXjEwkuqwsv5K2PT7Ax+3KCxhvCwqW8IyFBCbuhDLHlGD7jSL5jVY20EJKBDan2H+xRoldzkBoUOPReJH3PjWEj4/RwfdntAsFBfSbf4l3OF5gxfKzueX5go3f8y3fng1O1MD11CoIuFikkwBiXpKdp1HaG55q4uPn/OMs8UaG1lKsL9riYVJZUS69XW5WVRcTDSIkfQhQBgq42CaTv6DMlvf4xBizlO2d6hL9CwhPx3A==EXAMPLE 5
Farmer John’s tractor, traveling at 3 m/s, pulls a rope attached to a bale of hay through a pulley. With dimensions as indicated in Figure 3.70, how fast is the bale rising when the tractor is 5 m from the bale?
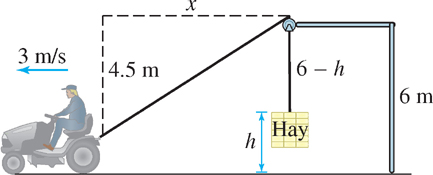
Solution
Step 1. Assign variables and restate the problem. Let \(x\) be the horizontal distance from the tractor to the bale of hay, and let \(h\) be the height above ground of the top of the bale. The tractor is 5 m from the bale when \(x = 5\), so we can restate the problem as follows:
\[ \boxed{\text{Compute }\left.\dfrac{dh}{dt}\right|_{x=5}\text{ given that }\dfrac{dx}{dt} = 3\text{ m/s}} \]
Step 2. Find an equation relating the variables and differentiate.
Let \(L\) be the total length of the rope. From Figure 3.70 (using the Pythagorean Theorem),
\[ L=\sqrt{x^2+4.5^2}+(6-h) \]
Although the length \(L\) is not given, it is a constant, and therefore \(\frac{dL}{dt} = 0\). Thus,
\[ \frac{dL}{dt} = \frac{d}{dt}\left(\sqrt{x^2+4.5^2}+(6-h)\right) = \frac{x\frac{dx}{dt}}{\sqrt{x^2+4.5^2}} - \frac{dh}{dt} = 0\tag{5} \]
199
Step 3. Use the given data to find the unknown derivative.
Apply Eq. (5) with \(x = 5\) and \(\frac{dx}{dt} = 3\). The bale is rising at the rate
\[ \frac{dh}{dt} = \frac{x\frac{dx}{dt}}{\sqrt{x^2+4.5^2}} = \frac{(5)(3)}{\sqrt{5^2+4.5^2}}\approx 2.23\text{ m/s} \]
3.11.1 Section 3.11 Summary
- Related-rate problems present us with situations in which two or more variables are related and we are asked to compute the rate of change of one of the variables in terms of the rates of change of the other variable(s).
- Draw a diagram if possible. It may also be useful to break the solution into three steps:
Step 1. Assign variables and restate the problem.
Step 2. Find an equation that relates the variables and differentiate.
This gives us an equation relating the known and unknown derivatives. Remember not to substitute values for the variables until after you have computed all derivatives.
Step 3. Use the given data to find the unknown derivative.
- The two facts from geometry arise often in related-rate problems: Pythagorean Theorem and the Theorem of Similar Triangles (ratios of corresponding sides are equal).